Regression

분석의 가장 기초가 되는 기법이다.

회귀분석의 사전적 뜻 :

회귀(영어: regress 리그레스[*****])의 원래 의미는 옛날 상태로 돌아가는 것을 의미한다. 영국의 유전학자 프랜시스 골턴은 부모의 키와 아이들의 키 사이의 연관 관계를 연구하면서 부모와 자녀의 키사이에는 선형적인 관계가 있고 키가 커지거나 작아지는 것보다는 전체 키 평균으로 돌아가려는 경향이 있다는 가설을 세웠으며 이를 분석하는 방법을 “회귀분석”이라고 하였다. 이러한 경험적 연구 이후, 칼 피어슨은 아버지와 아들의 키를 조사한 결과를 바탕으로 함수 관계를 도출하여 회귀분석 이론을 수학적으로 정립하였다.

Source: -위키피디아: https://ko.wikipedia.org/wiki/%ED%9A%8C%EA%B7%80_%EB%B6%84%EC%84%9D

So What ?

하나 이상의 ‘입력’변수와 ‘출력’변수 간의 관계를 설명하는 것.

입력 변수에 대한 값을 연결하여 ‘출력’변수에 대한 값을 예측하는 함수생성이 가능하다는 이야기.

예시 그래프)

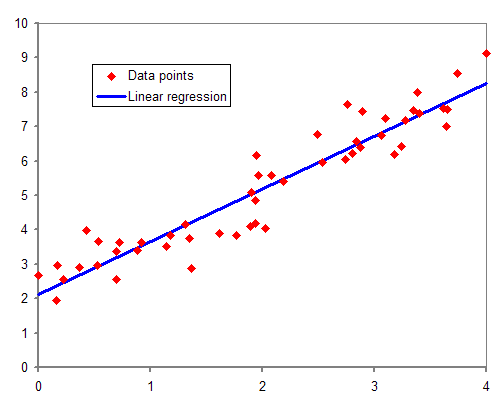
• 전형적인 회귀 분석 그래프다. 파란색 추세선은 데이터의 경향에 따른 Trend Line을 그려 놓은 것.

• 직선이기 때문에 Linear (선형)이란 말이 붙어서 리니어 리그레션 또는 선형회귀라고 한다.

통계적 정의에 따른 회귀분석의 전제조건 정리

선형성	독립변수와 종속변수가 선형관계여야 한다. 종속변수를 독립변수와 회귀 계수의 선형적인 조합으로 표현 가능하다. 산점도 Scatter Plot을 통해 잘 확인 가능
독립성	잔차와 독립변수의 값이 서로 독립이어야 한다.
등분산성	잔차의 분산이 독립변수와 무관하게 일정해야한다. 잔차가 고르게 분포해야함을 가정한다.
정규성	잔차항이 가우시안 정규분포를 따라야한다.
비상관성	잔차끼리 상관이 없음을 뜻한다.

회귀분석의 독립성, 등분산성(분산, 산점도), 정규성(QQ-plot), 비상관성(더빈 왓슨 통계량)

=> 모형의 적합도 검정 시작~

회귀분석의 통계적 유의성 검정 방법

=> F검정을 통한 통계적 유의성 검정

• F검정 통계량이 클수록 회귀모형은 통계적으로 유의하다.

• F검정 통계량은 MSR(회귀제곱평균)과 MSE(잔차제곱평균)로 계산된다.

• F검정 통계 결과 P값이 나오는데, 이게 작으면 작을 수록 통계적으로 유의하다고 판단한다.

• P값(value)이 0.05보다 작으면 통계적으로 유의하다고 판단.

=> 회귀계수 산식

• 표를 좌표평면에 표현한 후 데이터의 분포 사이에 Y=aX+b 형태의 추세선을 정의하면

• 이를 통해 독립변수에 따른 종속변수의 값을 예측할 수 있다.

• 이때 Y는 종속변수이고 X는 독립변수이며 a는 기울기, b는 X가 0일 때의 Y값, 즉 Y축의 절편이다.

• a는 회귀계수, b는 파라미터라고도 불린다.

=>왜 ‘잔차 제곱의 합’인가?

• 잔차는 양수가 될 수도 있고 음수가 될 수도 있어 잔차합을 사용할 경우

• 잔차합이 0이 되는 추세선이 무수히 많이 발견될 수 있기 때문이다.

=>회귀분석의 알고리즘 예시

• 최소제곱법을 통해 파라미터를 추정하고 추정된 파라미터를 통해 추세선을 그려 값을 예측

• 회귀분석의 기본 알고리즘이다. 최소제곱법이란 실제 관측치와 추세선에 의해 예측된 점 사이의 거리

• 즉 오차를 제곱해 더한 값을 최소화하는 것이다. 좌표평면상에서 다양한 추세선이 그려질 수는 있지만, 잔차의 제곱 합이 최소가 되는 추세선이 가장 합리적인 추세선이고 이를 통해 회귀분석을 실행한다.

[출처] 빅분기 카페

작성자 표준랜즈님 자료를 가져와 재구성하였습니다.

이 글이 도움이 되셨다면 추천 클릭을 부탁드립니다 :)